Definisi Intuitif:
Keacakan bukan berarti “tanpa pola” atau “kacau total”. Keacakan adalah ketidakpastian hasil individual meski kita bisa memprediksi pola jangka panjang.
Contoh Mudah:
# Simulasi lempar koin untuk menunjukkan pola jangka panjang
set.seed(123)
n_flips <- 1000
flips <- sample(c("Head", "Tail"), n_flips, replace = TRUE)
# Proporsi Head secara kumulatif
cumulative_heads <- cumsum(flips == "Head")
cumulative_prop <- cumulative_heads / (1:n_flips)
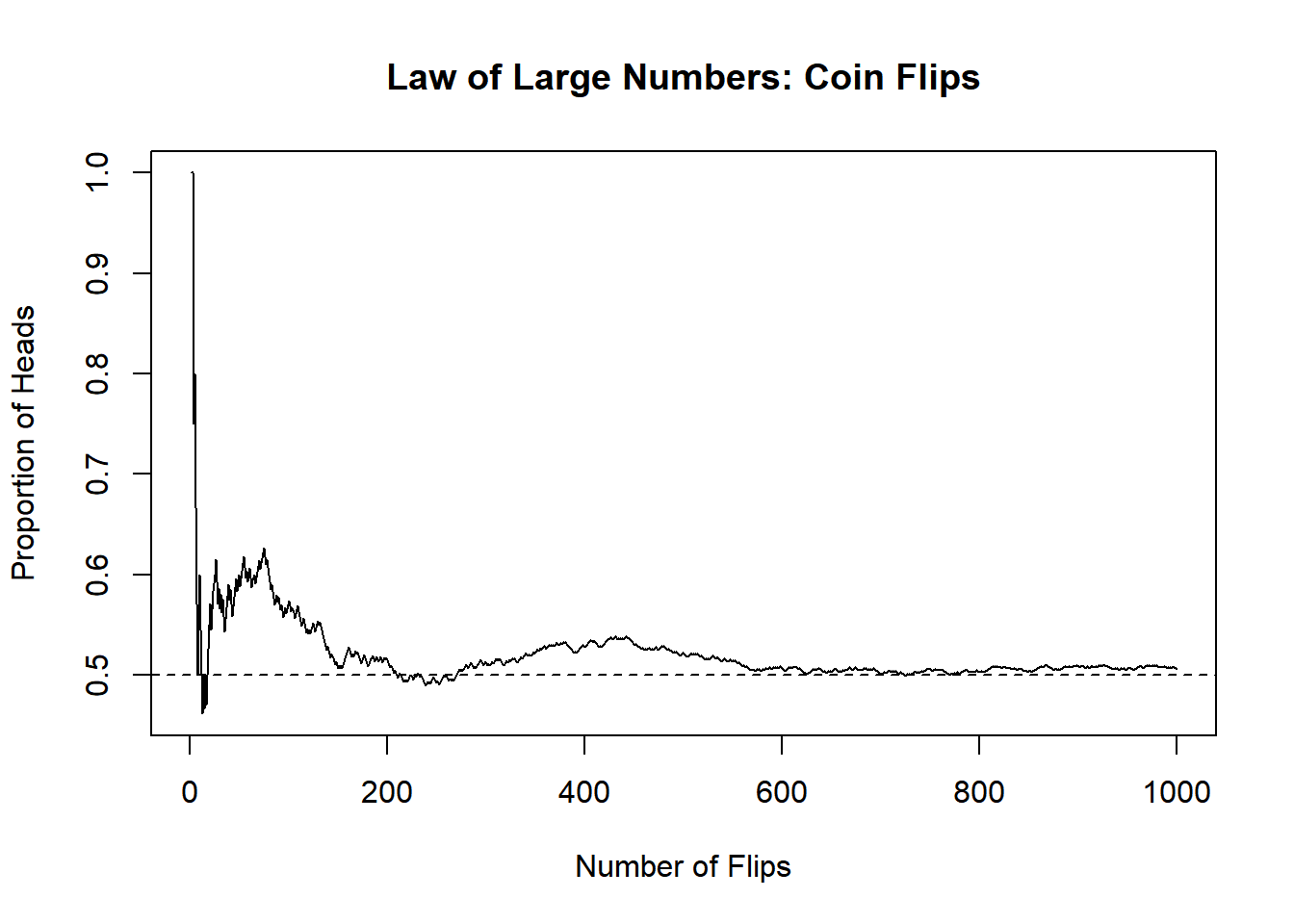
# Plot konvergensi ke 0.5
plot(1:n_flips, cumulative_prop, type = "l",
xlab = "Number of Flips",
ylab = "Proportion of Heads",
main = "Law of Large Numbers: Coin Flips")
abline(h = 0.5, lty = 2)
Eksperimen acak memiliki tiga komponen kunci:
Keacakan yang terjadi di alam:
Keacakan yang sengaja diciptakan:
Sistem deterministik yang terlihat acak:
Ruang sampel adalah kumpulan semua hasil yang mungkin dari suatu eksperimen acak. Seperti daftar lengkap semua kemungkinan yang bisa terjadi.
Ruang sampel, dilambangkan S atau Ω (omega), adalah himpunan semua hasil elementer (elementary outcomes) yang mungkin dari suatu eksperimen acak.
1. Melempar 1 koin: \[S = \{A, G\}\]
2. Melempar 1 dadu: \[S = \{1, 2, 3, 4, 5, 6\}\]
3. Melempar 2 koin: \[S = \{AA, AG, GA, GG\}\]
4. Memilih 1 mahasiswa dari 3 mahasiswa (Ali, Budi, Citra): \[S = \{Ali, Budi, Citra\}\]
1. Mengukur tinggi mahasiswa (dalam cm): \[S = \{x : 140 \leq x \leq 200\}\]
2. Waktu tunggu bus (dalam menit): \[S = \{t : t \geq 0\}\]
3. Suhu udara (dalam °C): \[S = \{T : -10 \leq T \leq 40\}\]
Prinsip:
Ruang sampel harus relevan dengan pertanyaan yang ingin dijawab.
Contoh: Melempar 2 koin
Jika pertanyaannya:
“Berapa banyak Head?”
[1] "0 Head" "1 Head" "2 Head"Jika pertanyaannya:
“Urutan hasil apa yang muncul?”
Jika eksperimen terdiri dari k tahap dengan n₁, n₂, …, nₖ kemungkinan hasil, maka total hasil = n₁ × n₂ × … × nₖ
Permutasi (urutan penting):
\[P(n,k) = \frac{n!}{(n-k)!}\]
Kombinasi (urutan tidak penting):
\[C(n,k) = \binom{n}{k} = \frac{n!}{k!(n-k)!}\]
# Fungsi helper
permutation <- function(n, k) factorial(n) / factorial(n - k)
combination <- function(n, k) factorial(n) / (factorial(k) * factorial(n - k))
# Contoh: Memilih 3 mahasiswa dari 10 untuk menjadi ketua, wakil, sekretaris
print(paste("Permutasi (urutan penting):", permutation(10, 3)))[1] "Permutasi (urutan penting): 720"[1] "Kombinasi (urutan tidak penting): 120"Mendaftar semua kemungkinan hasil secara eksplisit.
Contoh:
Melempar 2 dadu
S = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6),
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6),
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6),
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}Contoh:
Melempar 2 koin
# Visualisasi dengan R (sederhana)
# Koin 1: A atau G
# Koin 2: A atau G
hasil_2_koin <- expand.grid(Koin1 = c("A", "G"),
Koin2 = c("A", "G"))
print(hasil_2_koin) Koin1 Koin2
1 A A
2 G A
3 A G
4 G G
Berguna untuk menunjukkan hubungan antar kejadian dalam ruang sampel.
Kejadian adalah himpunan bagian dari ruang sampel yang menjadi fokus perhatian kita. Seperti memilih hasil-hasil tertentu yang kita minati dari semua kemungkinan hasil.
Kejadian (event) adalah subset dari ruang sampel S. Suatu kejadian dikatakan terjadi jika hasil eksperimen termasuk dalam himpunan kejadian tersebut.
Eksperimen:
Melempar 1 dadu, S = {1, 2, 3, 4, 5, 6}
Kejadian A:
“Muncul bilangan genap” \[A = \{2, 4, 6\}\]
Kejadian B:
“Muncul bilangan prima” \[B = \{2, 3, 5\}\]
Kejadian C:
“Muncul angka 3” \[C = \{3\}\] (kejadian sederhana)
Kejadian D:
“Muncul angka lebih dari 4” \[D = \{5, 6\}\]
Eksperimen:
Tes COVID-19 pada pasien
Ruang Sampel:
S = {(Test+, COVID+), (Test+, COVID-), (Test-, COVID+), (Test-, COVID-)}
Kejadian Penting:
# Simulasi data diagnosis
S <- expand.grid(Test = c("Positive", "Negative"),
COVID = c("Has", "NoHas"))
print("Sample Space for COVID Test:")[1] "Sample Space for COVID Test:"print(S) Test COVID
1 Positive Has
2 Negative Has
3 Positive NoHas
4 Negative NoHas# Define events
A <- S[S$Test == "Positive", ]
B <- S[S$COVID == "Has", ]
print("Event A (Test Positive):")[1] "Event A (Test Positive):"print(A) Test COVID
1 Positive Has
3 Positive NoHasDefinisi:
Kejadian yang hanya mengandung satu hasil elementer.
Contoh:
Definisi:
Kejadian yang mengandung lebih dari satu hasil elementer.
Contoh:
Definisi:
Kejadian yang pasti terjadi dalam setiap eksperimen.
Karakteristik:
Sama dengan ruang sampel (A = S)
Contoh:
Definisi:
Kejadian yang tidak mungkin terjadi.
Karakteristik:
Himpunan kosong (A = ∅)
Contoh:
Definisi:
Dua kejadian yang tidak dapat terjadi bersamaan.
Karakteristik:
A ∩ B = ∅
Contoh:
Definisi:
Terjadinya satu kejadian tidak mempengaruhi probabilitas kejadian lain.
Contoh:
Definisi:
Kejadian yang berisi semua hasil yang tidak termasuk dalam kejadian asli.
Notasi:
A’ atau A^c atau Ā
Karakteristik:
Contoh:
Definisi:
A ∪ B adalah kejadian yang terjadi jika A atau B (atau keduanya) terjadi.
Contoh:
Definisi:
A ∩ B adalah kejadian yang terjadi jika A dan B terjadi bersamaan.
Contoh:
Definisi:
A - B adalah kejadian yang terjadi jika A terjadi tetapi B tidak terjadi.
Contoh:
Definisi:
Kumpulan kejadian {A₁, A₂, …, Aₙ} membentuk partisi dari S jika:
Contoh:
Klasifikasi mahasiswa berdasarkan IPK
# Simulasi data IPK
set.seed(456)
ipk <- rnorm(100, mean = 3.0, sd = 0.5)
ipk <- pmax(0, pmin(4, ipk)) # Batasi antara 0-4
# Buat partisi
partition <- cut(ipk, breaks = c(0, 2.5, 3.0, 3.5, 4.0),
labels = c("Tidak Lulus", "Memuaskan", "Sangat Memuaskan", "Pujian"),
include.lowest = TRUE)
# Tampilkan distribusi
table(partition)partition
Tidak Lulus Memuaskan Sangat Memuaskan Pujian
14 35 32 19 Hukum yang menghubungkan operasi union, intersection, dan complement:
# Verifikasi De Morgan's Law dengan contoh
S <- 1:10
A <- c(2, 4, 6, 8, 10) # Bilangan genap
B <- c(1, 3, 5, 7, 9) # Bilangan ganjil
# Law 1: (A ∪ B)' = A' ∩ B'
union_AB <- union(A, B)
complement_union <- setdiff(S, union_AB)
complement_A <- setdiff(S, A)
complement_B <- setdiff(S, B)
intersection_complements <- intersect(complement_A, complement_B)
print("Verifikasi De Morgan Law 1:")[1] "Verifikasi De Morgan Law 1:"[1] "(A ∪ B)': "[1] "A' ∩ B': "[1] "Equal? TRUE"Simbol & Notasi yang Perlu Diingat:
1. Sebuah dadu bersisi 6 dilempar sekali. Tentukan ruang sampel dan jumlah ruang sampel dari percobaan ini.
2. Dalam pelemparan sebuah dadu, A adalah kejadian yang mungkin untuk angka genap. Tentukan anggota kejadian A, jumlah anggota kejadian A, dan peluang kejadian A.
3. Sebuah koin logam (ada sisi angka & gambar) dilempar dua kali. Berapa banyak anggota ruang sampel? Tuliskan semua elemennya. Berapa peluang munculnya 1 sisi gambar?
4. Sebuah dadu bersisi 6 dilempar satu kali. Berapa peluang munculnya bilangan prima?
5. Sebuah dadu bersisi 6 dilempar satu kali. Z adalah kejadian muncul bilangan ganjil dan Q adalah kejadian muncul bilangan prima.
Jawaban:
| Konsep | Definisi | Contoh Praktis |
|---|---|---|
| Keacakan | Ketidakpastian individual, prediktabilitas agregat | Lempar koin: tidak tahu hasil tunggal, tapi tahu proporsi jangka panjang ≈ 50% |
| Eksperimen Acak | Prosedur dengan hasil tidak pasti yang dapat diulang | Survei pelanggan, quality control, medical tests |
| Ruang Sampel | Semua kemungkinan hasil | Tergantung pertanyaan penelitian |
| Kejadian | Subset ruang sampel yang menarik | “Customer puas”, “Produk cacat”, “Test positif” |
| Partisi | Kejadian saling lepas dan exhaustive | Klasifikasi berdasarkan kategori yang tidak tumpang tindih |
Strategi Pemecahan Masalah: