1 Understanding the World with Data

1.1 Apa itu Data?

Data adalah informasi tentang individu/objek/unit observasi dalam bentuk angka, teks, gambar, atau sinyal yang dianalisis untuk menjawab pertanyaan penelitian atau bisnis.

Note

Definisi merujuk Agresti Statistics: The Art and Science of Learning from Data.

1.1.1 Contoh Data dalam Kehidupan Sehari-hari

1. Data Tabel (Structured Data)

Contoh tabel di atas menunjukkan data mahasiswa dengan variabel:

Name: data nominal (kategori tanpa urutan)
Gender: data nominal (Male/Female)
Height: data kontinu (dapat diukur dengan presisi tinggi)
Weight: data kontinu (berat badan dalam kg)
Religion: data nominal (kategori kepercayaan)
Age: data diskret (usia dalam tahun penuh)

2. Data Visual/Gambar (Unstructured Data)

Gambar burung ini adalah data unstructured yang bisa dianalisis untuk:

Klasifikasi spesies menggunakan machine learning
Analisis perilaku hewan
Penelitian biodiversitas

1.1.2 Klasifikasi Tipe Data

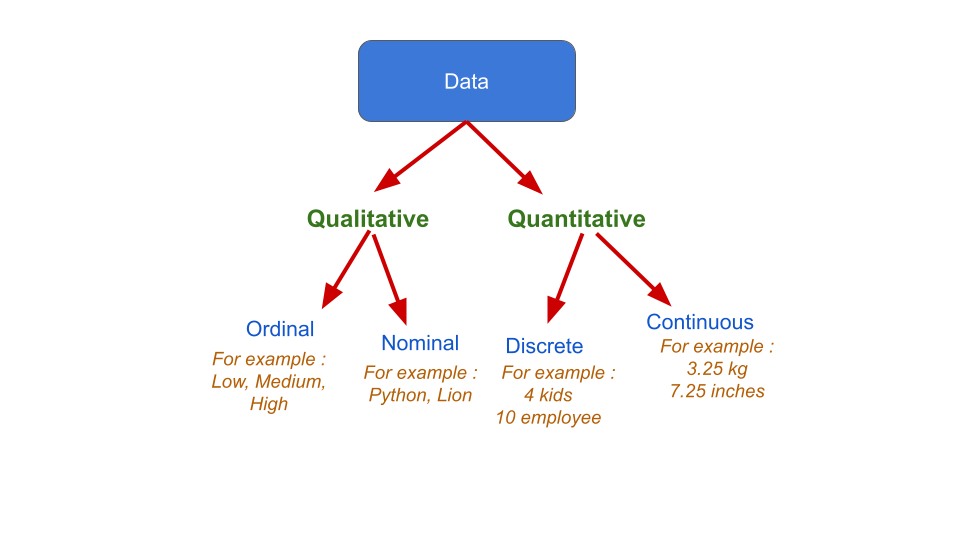
1.1.2.1 Data Kualitatif (Categorical)

1. Nominal: Kategori tanpa urutan natural

Contoh: Warna (merah, biru, hijau), Jenis kelamin (L/P), Agama
Tidak bisa diurutkan atau diberi ranking
Hanya bisa dihitung frekuensinya

2. Ordinal: Kategori yang bisa diurutkan

Contoh: Tingkat pendidikan (SD < SMP < SMA < S1), Rating kepuasan (tidak puas < cukup < puas < sangat puas)
Bisa diurutkan tapi jarak antar kategori tidak sama
Dapat menggunakan median sebagai ukuran tengah

1.1.2.2 Data Kuantitatif (Numerical)

3. Diskret: Hitungan bilangan bulat

Contoh: Jumlah anak (0, 1, 2, 3, …), Jumlah karyawan, Jumlah produk terjual
Tidak bisa berupa pecahan
Hasil dari menghitung (counting)

4. Kontinu: Bilangan riil pada rentang tertentu

Contoh: Tinggi badan (170.5 cm), Berat (65.7 kg), Suhu (25.3°C)
Bisa berupa pecahan dengan presisi tak terbatas
Hasil dari mengukur (measuring)

1.1.3 Skala Pengukuran

1.1.3.1 Skala Interval

Selisih antar nilai bermakna dan konsisten
Titik nol tidak absolut (arbitrary zero point)
Contoh: Suhu Celsius (0°C tidak berarti “tidak ada suhu”)
Operasi: penjumlahan dan pengurangan valid
Tidak bisa menghitung rasio (20°C bukan 2x lebih panas dari 10°C)

1.1.3.2 Skala Rasio

Selisih dan rasio antar nilai bermakna
Memiliki titik nol absolut (true zero point)
Contoh: Tinggi badan, berat, pendapatan, jarak
Operasi: semua operasi matematika valid
Bisa menghitung rasio (berat 60kg adalah 2x dari 30kg)

1.1.4 Data Tidak Terstruktur (Unstructured Data)

Karakteristik:

Tidak mengikuti format tabel yang terorganisir
Memerlukan teknik khusus untuk analisis
Volume sangat besar (big data)

Contoh dan Aplikasi:

Teks: Review produk, media sosial, dokumen → Sentiment analysis, topic modeling
Audio: Rekaman suara, musik → Speech recognition, music classification
Video: Film, surveillance → Object detection, behavior analysis
Gambar: Foto produk, medical imaging → Image classification, medical diagnosis

1.2 Apa itu Statistika?

“Statistics is the art and science of learning from data.” — Agresti

Statistika adalah ilmu yang mencakup pengumpulan, peringkasan, pemodelan, dan inferensi dari data untuk membuat keputusan yang berdasar bukti.

1.2.1 Interpretasi Visual Data

Contoh 1: Rating Produk E-commerce

Dari grafik ulasan pembeli di atas:

4.8/5.0: Rating rata-rata sangat tinggi
100% pembeli merasa puas: Indikator kualitas produk excellent
12 rating, 10 ulasan: Sample size cukup untuk validitas
Distribusi rating: Mayoritas 5 bintang (10), sedikit 4 bintang (2)
Interpretasi bisnis: Produk berkualitas tinggi, customer satisfaction excellent

Contoh 2: Data Demografi iPhone

Data spesifikasi produk teknologi:

Processor: Apple A18 Chip (data nominal - jenis processor)
Storage: 128GB (data diskret - kapasitas penyimpanan)
Battery: 3561mAh (data kontinu - kapasitas baterai)
Camera: 48MP main, 12MP front (data diskret - resolusi kamera)
Screen: 6.1” Super Retina XDR OLED (data kontinu - ukuran layar)

1.2.2 Cabang Utama Statistika

1.2.2.1 1. Statistika Deskriptif

Tujuan: Meringkas dan menampilkan data Metode:

Tabel: Distribusi frekuensi, crosstab
Grafik: Histogram, boxplot, scatter plot, pie chart
Ukuran numerik: Mean, median, modus, standar deviasi, range

Contoh Aplikasi:

Dashboard penjualan bulanan
Profil demografis pelanggan
Rangkuman kinerja karyawan

1.2.2.2 2. Statistika Inferensial

Tujuan: Membuat kesimpulan tentang populasi berdasarkan sampel Metode:

Estimasi: Point estimate, confidence interval
Uji Hipotesis: t-test, chi-square test, ANOVA
Regresi: Memprediksi hubungan antar variabel

Contoh Aplikasi:

Survei politik: Prediksi hasil pemilu dari sample
Quality control: Menentukan produk memenuhi standar
A/B Testing: Membandingkan efektivitas dua strategi marketing

1.2.3 Contoh Penerapan dalam Konteks Pendidikan

Analisis Statistik pada Data Pendidikan:

Statistika Deskriptif:

Jumlah sekolah per provinsi (data diskret)
Distribusi jenjang pendidikan (data ordinal: SD < SMP < SMA)
Rasio guru-siswa per daerah (data rasio)

Statistika Inferensial:

Estimasi kebutuhan guru nasional dari data sampel daerah
Uji hipotesis: Apakah rasio guru-siswa berbeda signifikan antar provinsi?
Prediksi pertumbuhan jumlah sekolah 5 tahun ke depan

1.3 Probabilitas: Kerangka Mengukur Ketidakpastian

Probabilitas adalah sistem matematis untuk mengkuantifikasi dan menganalisis ketidakpastian dalam berbagai fenomena.

1.3.1 Aplikasi dalam Kehidupan Sehari-hari

1. Prediksi Cuaca

“60% kemungkinan hujan” = P(Hujan) = 0.6
Berdasarkan data historis pola cuaca serupa
Membantu perencanaan aktivitas outdoor

2. Diagnosa Medis

“Terapi ini memiliki 80% tingkat kesembuhan”
Berdasarkan data klinis dari pasien sebelumnya
Membantu dokter dan pasien membuat keputusan treatment

3. Investasi Keuangan

“Portfolio ini memiliki risiko 15% mengalami kerugian”
Berdasarkan analisis historis pergerakan pasar
Membantu investor mengelola risiko

4. Industri Asuransi

Menghitung premi berdasarkan probabilitas klaim
Data historis kecelakaan, kesehatan, bencana
Menentukan tarif yang profitable namun kompetitif

1.3.2 Peran Krusial dalam Statistika

1.3.2.1 1. Dasar Teoritis Inferensi

Sampling distribution: Bagaimana statistik sampel terdistribusi
Central Limit Theorem: Distribusi mean sampel mendekati normal
Confidence interval: Rentang nilai parameter populasi yang mungkin

1.3.2.2 2. Uji Hipotesis

P-value: Probabilitas mendapat hasil ekstrem jika H₀ benar
Type I error: Probabilitas menolak H₀ padahal benar (α)
Type II error: Probabilitas menerima H₀ padahal salah (β)
Power: Probabilitas menolak H₀ padahal salah (1-β)

1.3.2.3 3. Kuantifikasi Ketidakpastian

Standard error: Ukuran variabilitas estimasi
Margin of error: Rentang ketidakpastian dalam estimasi
Prediction interval: Rentang nilai prediksi individual

Tip

Contoh Lengkap - Survei Preferensi Produk:

Data: Survei 1.000 responden, 650 orang (65%) menyukai produk A

Statistika Deskriptif:

Proporsi sampel = 650/1000 = 0.65 (65%)

Statistika Inferensial dengan Probabilitas:

Estimasi proporsi populasi = 65%
Standard error = √[0.65(1-0.65)/1000] = 0.015
95% Confidence Interval = 65% ± 1.96(1.5%) = (62.1%, 67.9%)

Interpretasi: “Dengan tingkat kepercayaan 95%, proporsi populasi yang menyukai produk A berada antara 62.1% hingga 67.9%”

1.3.2.4 4. Pengambilan Keputusan Berbasis Data

Decision theory: Memilih tindakan optimal dengan ketidakpastian
Expected value: Nilai harapan dari berbagai skenario
Risk assessment: Evaluasi probabilitas dan dampak risiko

Contoh Aplikasi Bisnis:

Marketing: A/B testing dengan confidence interval
Finance: Value at Risk (VaR) menggunakan probabilitas kerugian
Operations: Quality control dengan sampling inspection
HR: Prediksi turnover karyawan berdasarkan data historis

1.4 Referensi

Agresti, A., Franklin, C., Klingenberg, B. (2018). Statistics: The Art and Science of Learning from Data. Pearson.
Mendenhall, W., Beaver, R. J., Beaver, B. M. (2013). Introduction to Probability and Statistics (14th ed.). Brooks/Cole.
Ott, R. L., Longnecker, M. (2010). An Introduction to Statistical Methods and Data Analysis (6th ed.). Brooks/Cole.
Lohr, S. L. (2010). Sampling: Design and Analysis (2nd ed.). Brooks/Cole.
Scheaffer, R. L., Mendenhall, W., Ott, L., Gerow, K. G. (2012). Elementary Survey Sampling (7th ed.). Brooks/Cole.