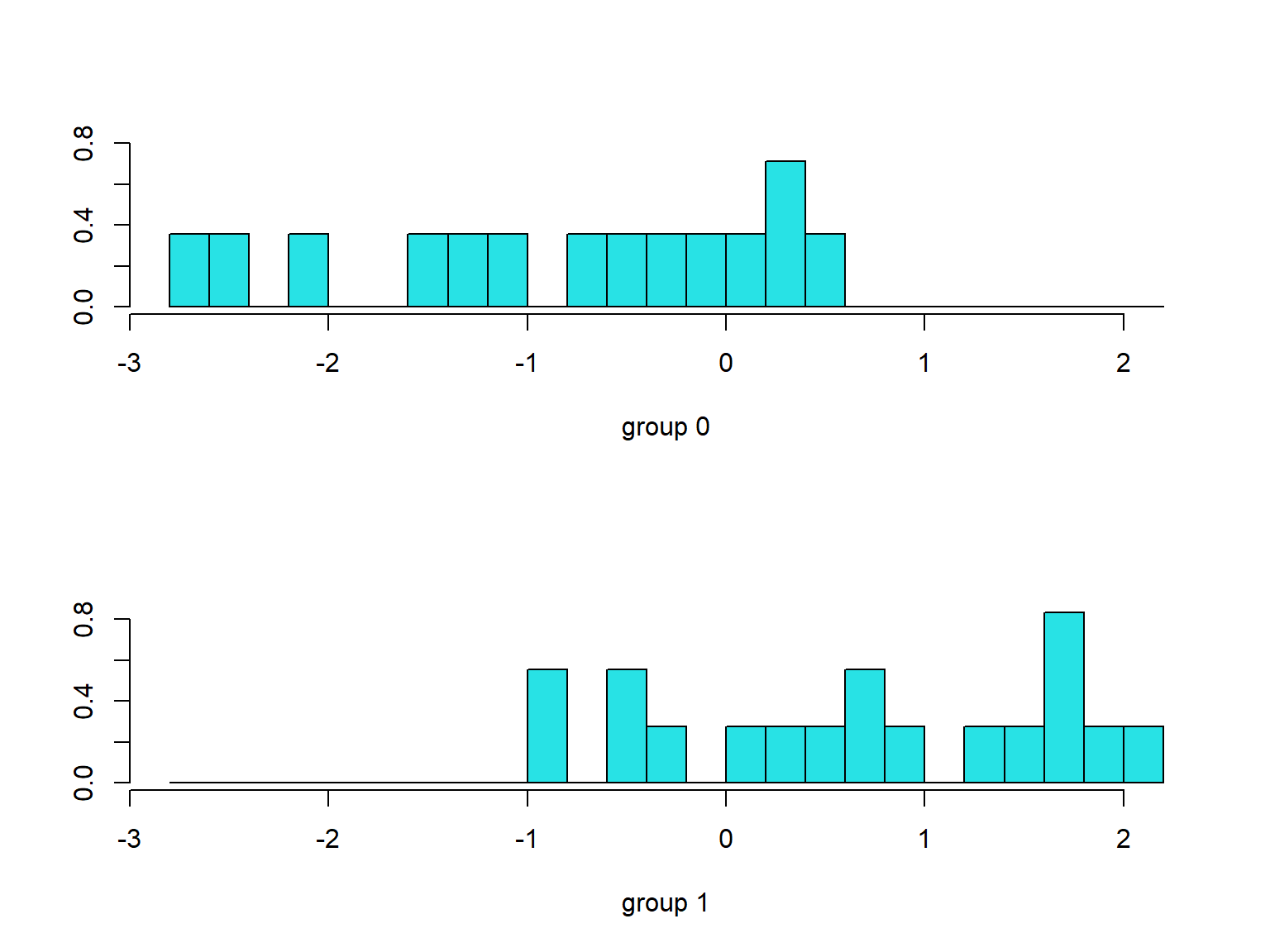# Discriminant Analysis
## Analisis Diskriminan Dua Grup
### Data
```{r}
library(readxl)
pinjaman <- read_excel("Data/pinjaman.xlsx")
head(pinjaman,10)
```
```{r}
str(pinjaman)
```
```{r}
pinjaman$Y <- as.factor(pinjaman$Y)
str(pinjaman)
```
```{r}
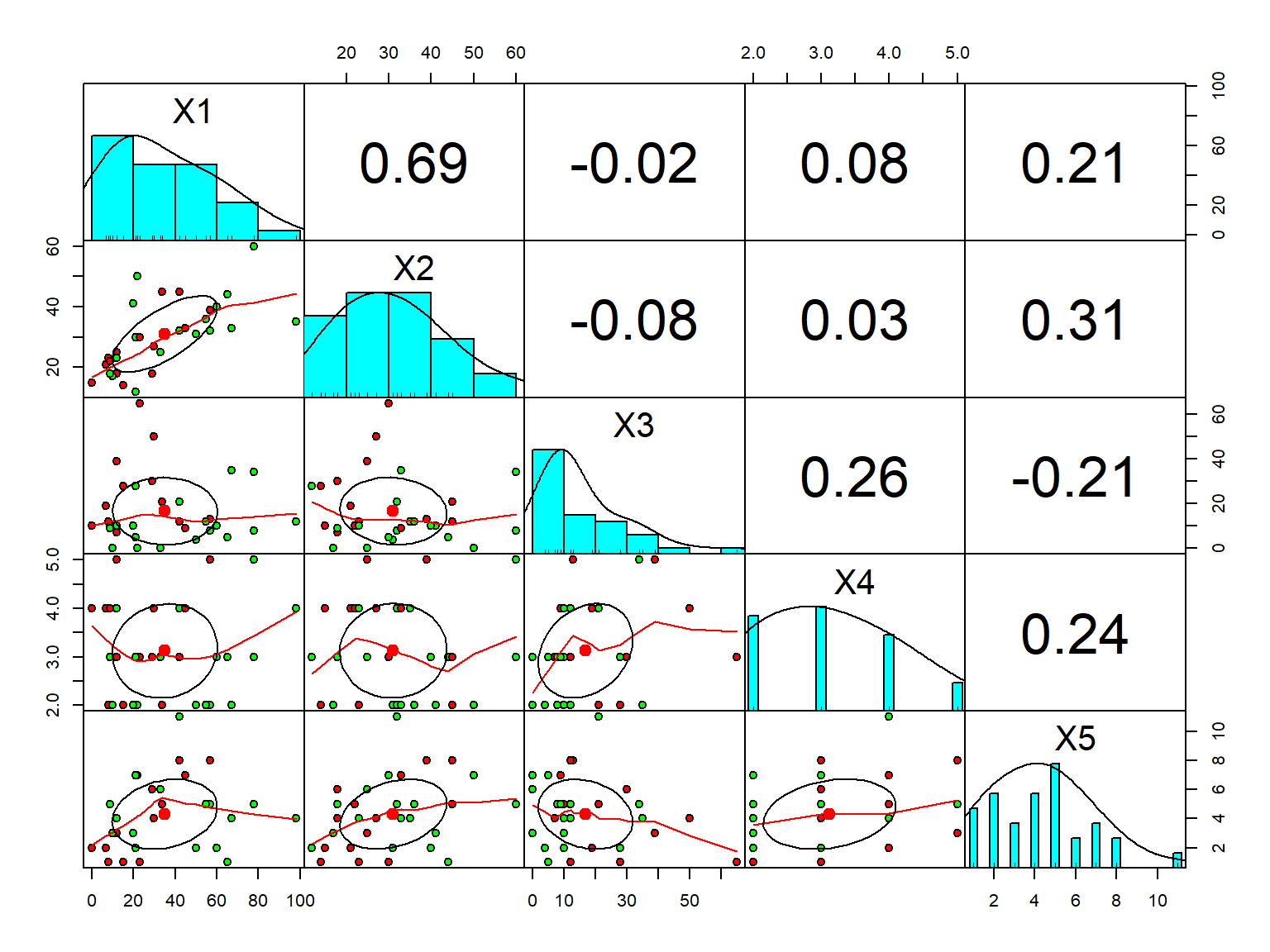
library(psych)
pairs.panels(pinjaman[1:5],
gap = 0,
bg = c("red", "green")[pinjaman$Y],
pch = 21)
```
### Pemodelan Linier
```{r}
library(MASS)
modellda1 <- lda(Y ~ X1 + X2 + X3 + X4 + X5, data=pinjaman)
modellda1
```
### Uji Signifikansi Fungsi Diskriminan
```{r}
m <- manova(cbind(pinjaman$X1,pinjaman$X2,pinjaman$X3,
pinjaman$X4,pinjaman$X5) ~ pinjaman$Y)
summary(m, test = 'Wilks')
```
### Akurasi
```{r}
p <- predict(modellda1, pinjaman)
ldahist(data = p$x, g = pinjaman$Y)
```
```{r}
library(caret)
confusionMatrix(p$class,pinjaman$Y)
```
```{r}
mean(p$class==pinjaman$Y)
```
```{r}
#install.packages("klaR")
library(klaR)
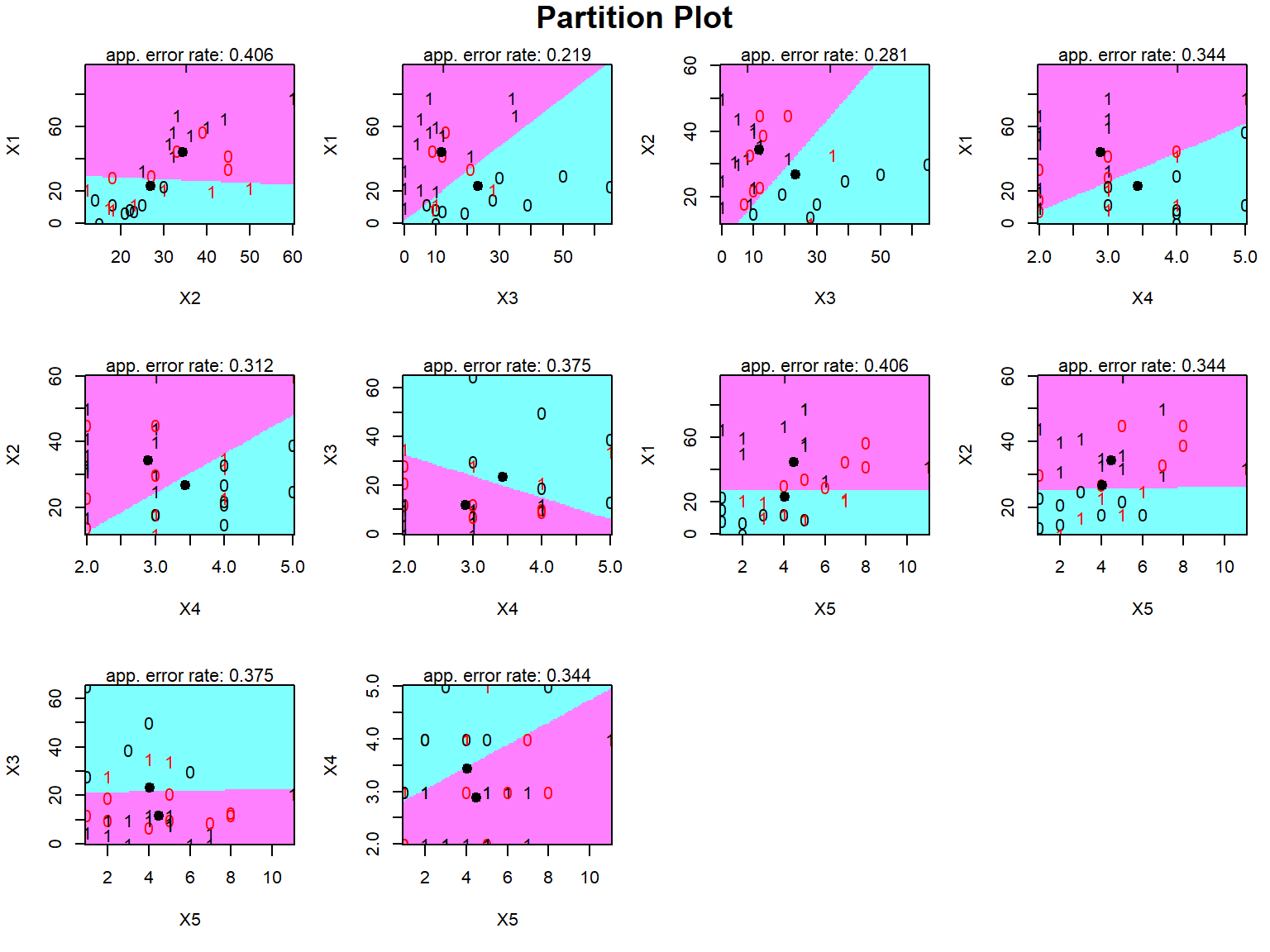
#Partition plot
partimat(Y~., data = pinjaman, method = "lda")
```
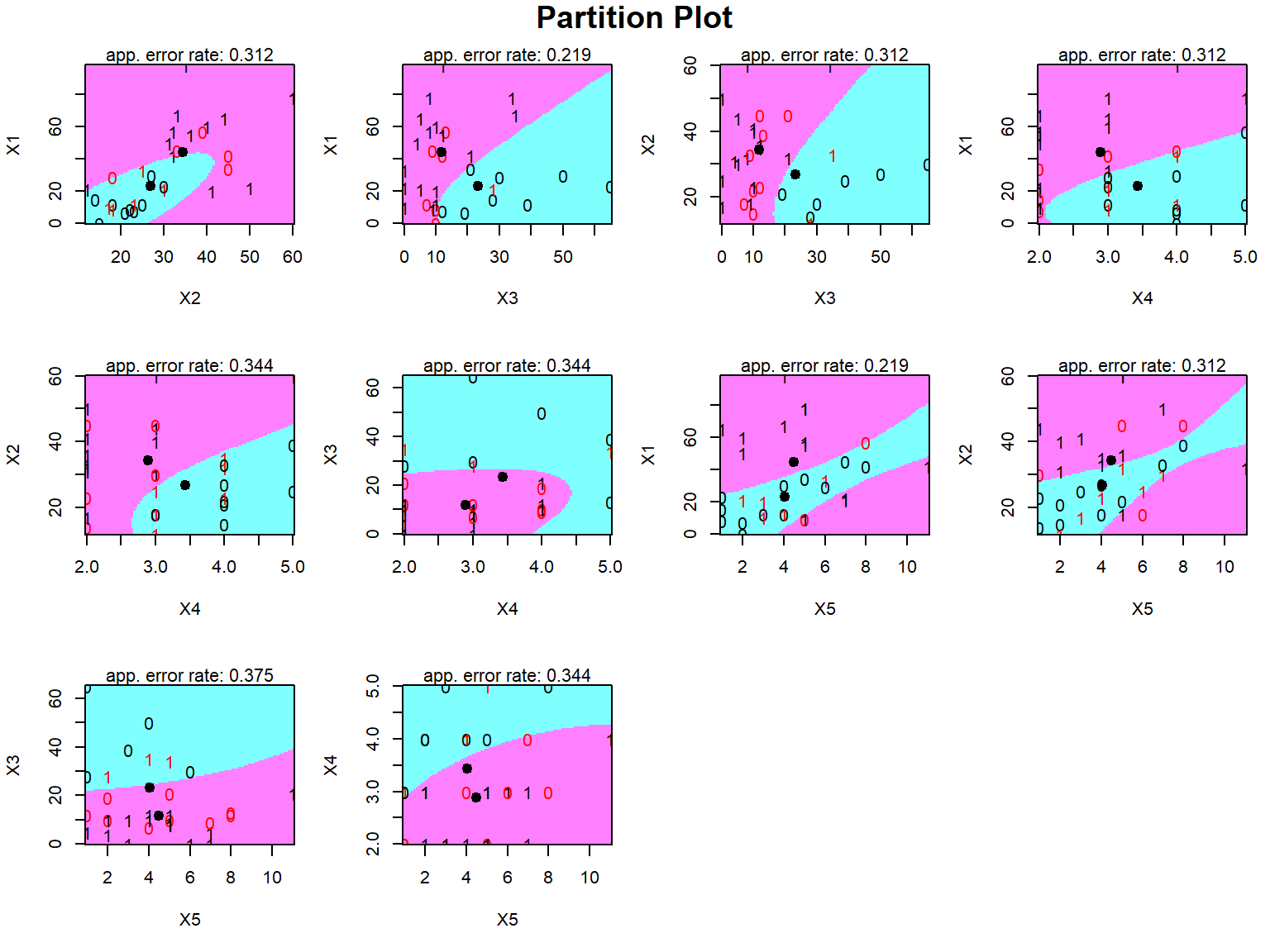
```{r}
partimat(Y~., data = pinjaman, method = "qda")
```
### Pemodelan Quadratik
```{r}
modellda2 <- qda(Y ~ X1 + X2 + X3 + X4 + X5, data=pinjaman)
modellda2
```
```{r}
p <- predict(modellda2, pinjaman)
mean(p$class==pinjaman$Y)
```
### Tipe Diskriminan Lainnya
```{r}
# Mixture discriminant analysis - MDA
# install.packages("mda")
library(mda)
modellda3 <- mda(Y ~ X1 + X2 + X3 + X4 + X5, data=pinjaman)
p <- predict(modellda3, pinjaman)
mean(p==pinjaman$Y)
```
```{r}
# Flexible discriminant analysis - FDA
modellda4 <- fda(Y ~ X1 + X2 + X3 + X4 + X5, data=pinjaman)
p <- predict(modellda4, pinjaman)
mean(p==pinjaman$Y)
```
```{r}
# Regularized discriminant analysis - RDA
modellda5 <- rda(Y ~ X1 + X2 + X3 + X4 + X5, data=pinjaman)
p <- predict(modellda5, pinjaman)
mean(p$class==pinjaman$Y)
```
## Analisis Diskriminan Tiga Grup
### Data
```{r}
data("iris")
head(iris)
```
```{r}
str(iris)
```
```{r}
library(MASS)
lda.iris <- lda(Species ~ ., iris)
lda.iris
```
### Uji Signifikansi Fungsi Diskriminan
```{r}
m <- manova(cbind(iris$Sepal.Length,iris$Sepal.Width,iris$Petal.Length,
iris$Petal.Width) ~ iris$Species)
summary(m, test = 'Wilks')
```
### Akurasi
```{r}
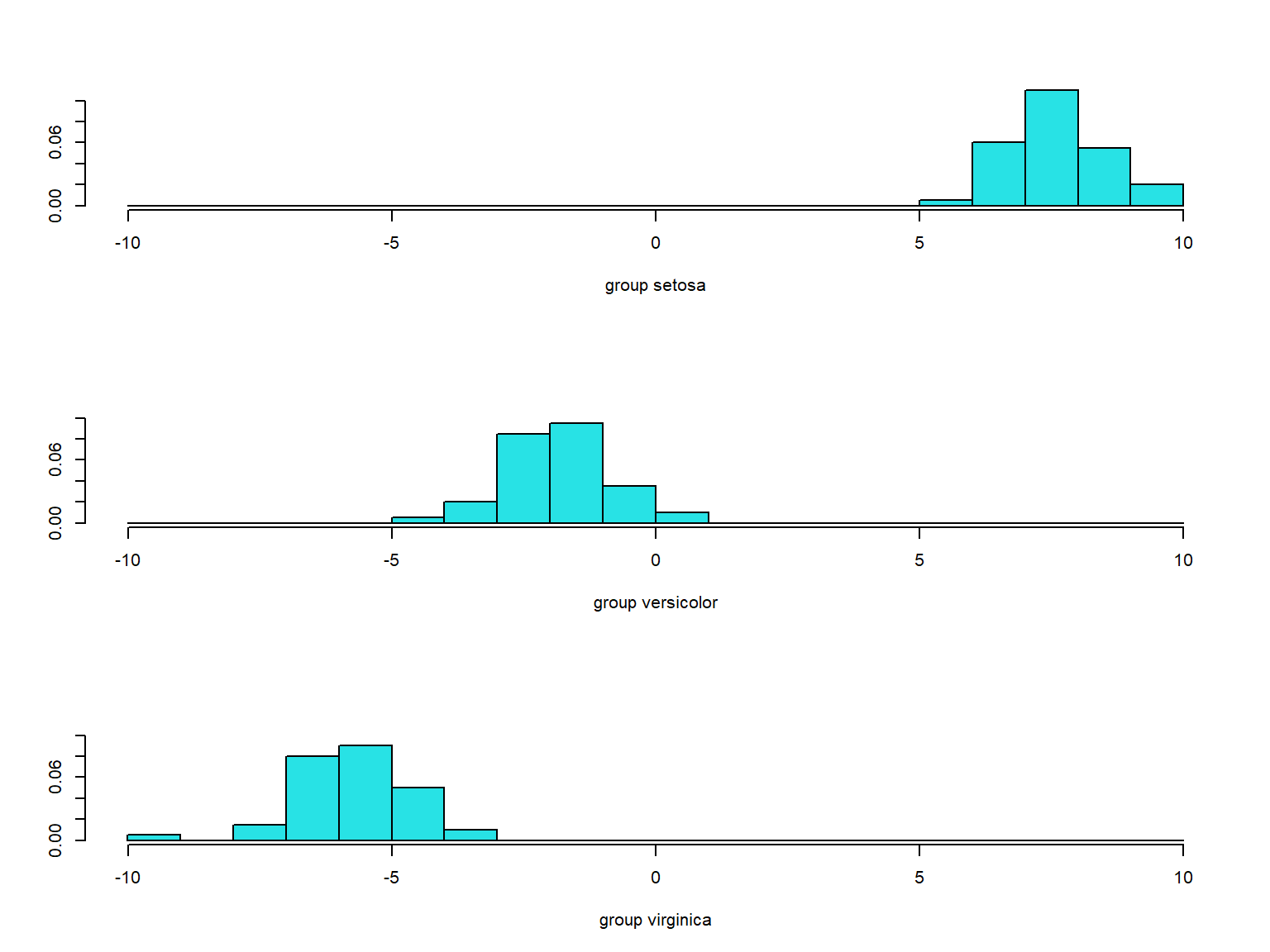
p <- predict(lda.iris, iris)
ldahist(data = p$x, g = iris$Species)
```
```{r}
table(p$class,iris$Species)
```
```{r}
mean(p$class==iris$Species)
```
### Visualisasi
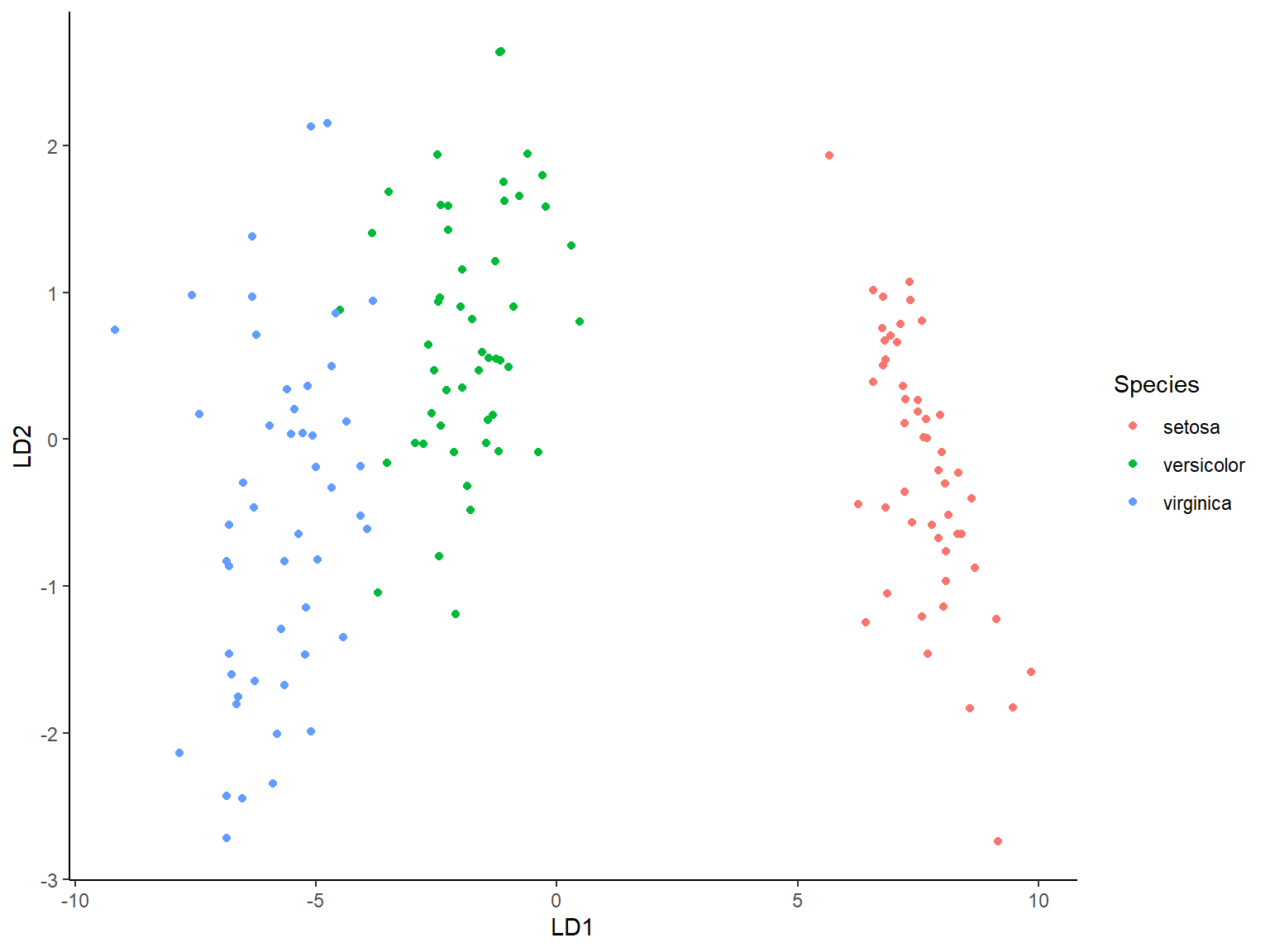
```{r}
library(ggplot2)
lda.data <- cbind(iris, p$x)
ggplot(lda.data, aes(LD1, LD2)) +
geom_point(aes(color = Species)) + theme_classic()
```
### Pemodelan Quadratik
```{r}
qda.iris <- qda(Species ~ ., data=iris)
qda.iris
p <- predict(qda.iris, iris)
mean(p$class==iris$Species)
```
### Tipe Diskriminan Lainnya
```{r}
# Mixture discriminant analysis - MDA
# install.packages("mda")
library(mda)
mda.iris <- mda(Species ~ ., data=iris)
mda.iris
p <- predict(mda.iris, iris)
mean(p==iris$Species)
```
```{r}
# Flexible discriminant analysis - FDA
fda.iris <- fda(Species ~ ., data=iris)
fda.iris
p <- predict(fda.iris, iris)
mean(p==iris$Species)
```
```{r}
# Regularized discriminant analysis - RDA
rda.iris <- rda(Species ~ ., data=iris)
rda.iris
p <- predict(rda.iris, iris)
mean(p$class==iris$Species)
```